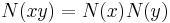Composition algebra

In mathematics, a composition algebra A over a field K is a unital (but not necessarily associative) algebra over K together with a nondegenerate quadratic form N which satisfies

for all x and y in A.  The quadratic form N is often referred to as a norm on A.  Composition algebras are also called normed algebras (not to be confused with normed algebras in the sense of functional analysis).

Structure theorem

Every composition algebra over a field K can be obtained by repeated application of the Cayley–Dickson construction starting from K (if the characteristic of K is different from 2) or a 2-dimensional composition subalgebra (if char(K) = 2).  The possible dimensions of a composition algebra are 1, 2, 4, and 8.

• 1-dimensional composition algebras only exist when char(K) ≠ 2.
• Composition algebras of dimension 1 and 2 are commutative and associative.
• Composition algebras of dimension 2 are either quadratic field extensions of K or isomorphic to .
• Composition algebras of dimension 4 are called quaternion algebras.  They are associative but not commutative.
• Composition algebras of dimension 8 are called octonion algebras.  They are neither associative or commutative.

See also

• Normed division algebra
• Hurwitz's theorem (normed division algebras)

References

• Harvey, F. Reese (1990). Spinors and Calibrations. San Diego: Academic Press. ISBN 0-12-329650-1. 
• Schafer, Richard D. (1995). An introduction to non-associative algebras. Dover Publications. pp. 72–75. ISBN 0-486-68813-5. 
• Springer, T. A.; F. D. Veldkamp (2000). Octonions, Jordan Algebras and Exceptional Groups. Springer-Verlag. ISBN 3-540-66337-1.